From this post on, I've decided to include a little "Prerequisites" section because I don't really cover concepts in any particular order: I just post what I find interesting. However, the prerequisites section WILL include a basic definition. If you are smart enough to figure out the rest from context, good for you. For today, we have Minimum Spanning Trees.
So what IS a Minimum Spanning Tree (MST from here on out)? For this, first we must define what is meant by a spanning tree.
Prerequisites
For this topic to make sense, you should be aware of a few things. If I have covered them on this blog, you can check that up, otherwise Google them before continuing! You have been warned.
- Basics of Graph Theory: You need to know the absolute essentials of Graphs, because that is where we are gonna construct Minimum Spanning Trees from. We are gonna work with undirected, connected, weighted graphs for this topic. A graph is a data structure consisting of elements called vertices or nodes and connecting elements called edges.
- Trees: Seriously? Trees? You can't see why that's necessary? Stop gaping and go learn it. Psst: I'm not talking about binary trees. These are trees in general. A tree is a subset of graphs where there are no cycles present.
Begin!
So what IS a Minimum Spanning Tree (MST from here on out)? For this, first we must define what is meant by a spanning tree.
In an undirected, weighted, connected graph (technically, aren't unconnected graphs expressible as multiple separate graphs? But I digress...), a spanning tree is the tree that results when you remove all cycles from the graph, in such a manner that all nodes stay connected. In other words, it is the set of edges that connect all nodes and do not form cycles.
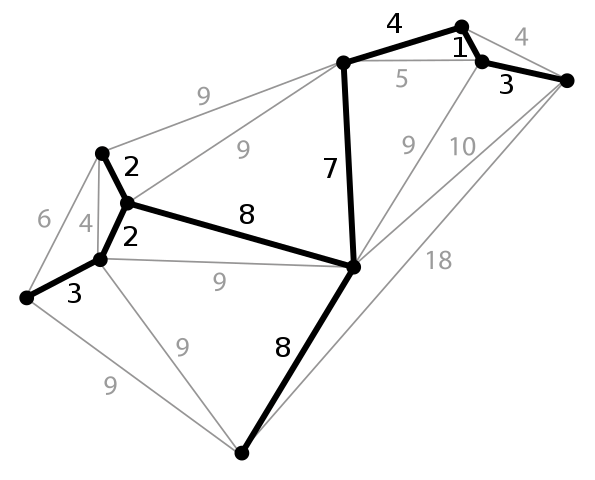
Now for a particular graph, there may be multiple spanning trees possible. Take the graph in question (assume all edges are weighted):
For this graph, this is one possible spanning tree (edges in red):
This is another:
Thus, it is plain that multiple spanning trees may exist for a graph. A spanning tree for 'n' nodes will have 'n-1' edges, however. This is because, if you assumed edges as directional (pointing from parent to child), every node will have ONE parent (no cycles, remember?), except one node, which will have no parent (picture it in your mind: any tree can be "hung" from a single node. That node will act as the "root", while all the other nodes will hang from it as "branches"). Thus, one edge will be associated with every node (the node and its "parent" edge) except the root node. Hence, n-1 edges.
It should be clear that spanning trees can be formed by eliminating cycles from the graph. We have the choice of eliminating cycles by removing any edge in the cycle. So what would happen if we chose to remove the maximum edge every time to eliminate a cycle? We would end up with the set of edges necessary to connect the graph with the minimum possible total sum. THIS is the Minimum Spanning Tree.
The MST is the spanning tree that has the minimum total edge-weight sum of all possible spanning trees. That's pretty much the definition given on Wikipedia, so chew on that.
The trouble is, there ARE multiple possible MSTs for a graph. For example, take a simple square graph (4 edges, 4 vertices, edges have equal weights). It is possible to generate 4 MSTs here, one each by removing any one edge (actually, in a graph with all edge-weights equal, the number of spanning trees and MSTs are the same: chew on that too). Anyhoo, in most cases it does not matter which MST we end up with, so long as the spanning tree we obtain DOES have the minimum weight sum.
In the case where all edge weights in the graph are unique, it is guaranteed that there is only one unique MST. I don't think I need to explain why that is so. Think about it.
For this graph, this is one possible spanning tree (edges in red):
This is another:
Thus, it is plain that multiple spanning trees may exist for a graph. A spanning tree for 'n' nodes will have 'n-1' edges, however. This is because, if you assumed edges as directional (pointing from parent to child), every node will have ONE parent (no cycles, remember?), except one node, which will have no parent (picture it in your mind: any tree can be "hung" from a single node. That node will act as the "root", while all the other nodes will hang from it as "branches"). Thus, one edge will be associated with every node (the node and its "parent" edge) except the root node. Hence, n-1 edges.
It should be clear that spanning trees can be formed by eliminating cycles from the graph. We have the choice of eliminating cycles by removing any edge in the cycle. So what would happen if we chose to remove the maximum edge every time to eliminate a cycle? We would end up with the set of edges necessary to connect the graph with the minimum possible total sum. THIS is the Minimum Spanning Tree.
The MST is the spanning tree that has the minimum total edge-weight sum of all possible spanning trees. That's pretty much the definition given on Wikipedia, so chew on that.
 |
| The MST of... that graph. Wow, that is a BIG graph. (Wikimedia) |
The trouble is, there ARE multiple possible MSTs for a graph. For example, take a simple square graph (4 edges, 4 vertices, edges have equal weights). It is possible to generate 4 MSTs here, one each by removing any one edge (actually, in a graph with all edge-weights equal, the number of spanning trees and MSTs are the same: chew on that too). Anyhoo, in most cases it does not matter which MST we end up with, so long as the spanning tree we obtain DOES have the minimum weight sum.
In the case where all edge weights in the graph are unique, it is guaranteed that there is only one unique MST. I don't think I need to explain why that is so. Think about it.
So what's the point?
Why find MSTs? Why do we need these... things? Why aren't we content? What do we seek? What is the meaning of life?
I'm sure you have a lot of questions. I can answer the first one. MSTs are useful wherever you need to minimize some "cost" of connecting multiple units. There is a simple example given over on that Wikipedia page, of a telecommunications company trying to connect telephones.
If that is not enough, MSTs are also useful in shortest-path calculations. What's the minimum amount of road needed to be traversed to go from a city to any other city? A tree guarantees a unique path between any two points along it (think of why that is so). Therefore, the MST contains ALL shortest paths in the graph. All you gotta do is traverse!
Okay, I'm convinced. How do we find them?
Whoa... hold your horses, cowboy. Never said I'd tell you that just yet! The science of finding MSTs is not a small one, and it will be covered in subsequent posts. If you simply cannot wait, however, there exist many algorithms that can aid in their discovery. At the time of writing this post, I know two of them: Kruskal's algorithm and Prim's algorithm. Google 'em, it'll be fun.




No comments:
Post a Comment